下沉帖，勿顶

guang3000

      出验证篇了！锁相环+带隙基准验证 ， 锁相环验证在9楼，带隙基准验证在17楼！

    闭环极点法是以系统左平面共轭复极点到原点斜率的倒数的绝对值β来判断系统稳定性的方法，β越大，系统就越稳定。在存在减幅振荡的时候，能较好的描述和量化系统的稳定性。

    若一个闭环系统阶跃响应出现减幅振荡，系统的闭环传输函数必然会出现左平面共轭复数根s = σ ±ωj，阶跃响应会出现一个衰减指数项，形式是 K × exp(σt) × sin(ωt) , 可以看作一个衰减的指数项乘以一个正常的sin函数。

      现在以图1的常见二级运放为例，说明如何在spectre中运用闭环极点法来分析运放的稳定性，在这里只调整电容的值来改变运放的稳定性 , 对运放进行闭环AC和pole-zero分析，再print pole-zero summary就可以看到零极点了。下面先把图表公式全部列出来，然后再进行具体分析。


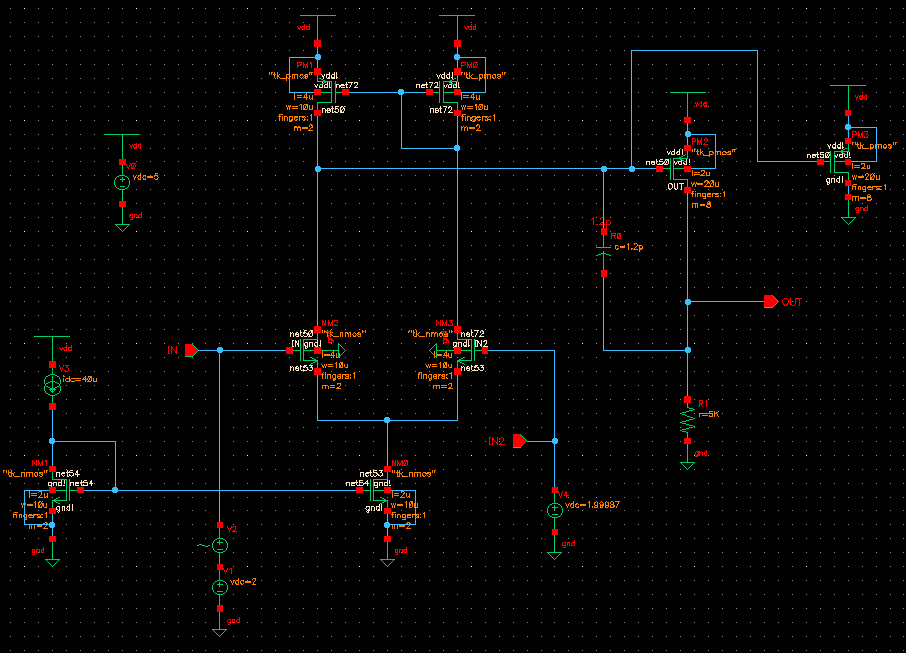
        图1 常见二级运放

############### 表1 系统稳定性和闭环极点分布的对应关系 #######################

                  实数极点                              共轭复极点

左平面       单调指数减幅（稳定）         减幅震荡（可能不稳定,视情况而定）

右平面       单调指数增幅（不稳定）      增幅震荡（不稳定）



### 表2 ：不同的相位裕度下，系统共轭复根的分布情况和对应的阶跃响应 ##########

注释：

β   :      比例因子，σ / ω 的绝对值
PM   :     相位裕度
σ    ： 闭环极点的实部，可以由spectre仿真得到
ω    ： 闭环极点的虚部，可以由spectre仿真得到


####################### 表3  用到的公式 ################################


公式1：u(t)= K1+K2 × exp(σt) × sin(ωt) , σ是减幅震荡的衰减因子,ω 是减幅震荡的频率

公式2 ： ωT= 2π ， T是减幅震荡的周期

公式3： σ= -1 / τ , τ为时间常数


###############################################################################

   


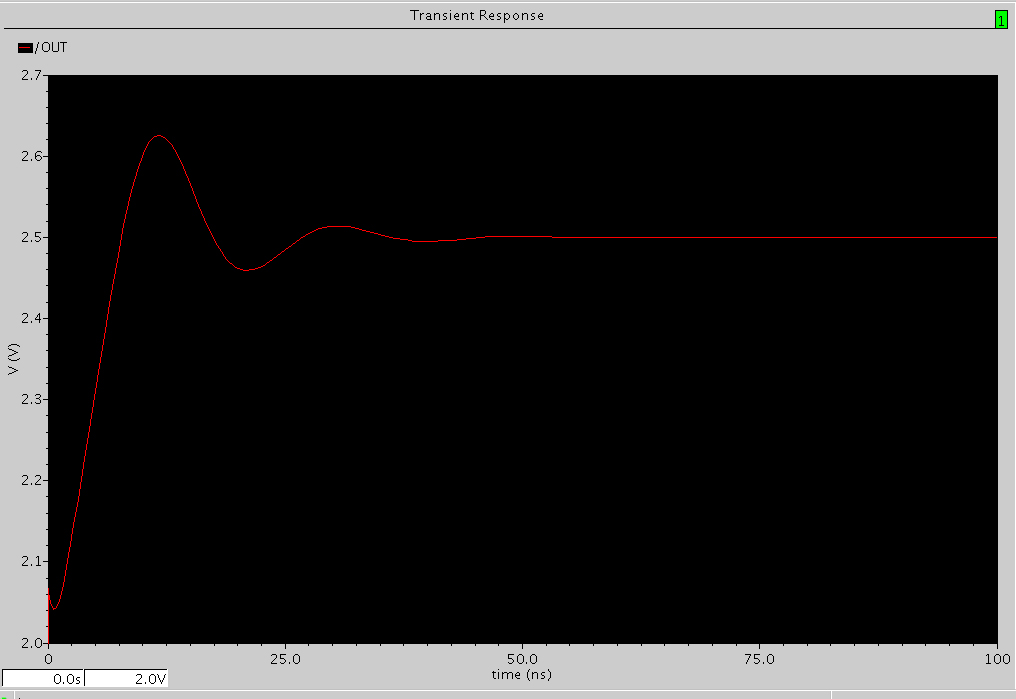
       图2 PM=45度时的阶跃响应



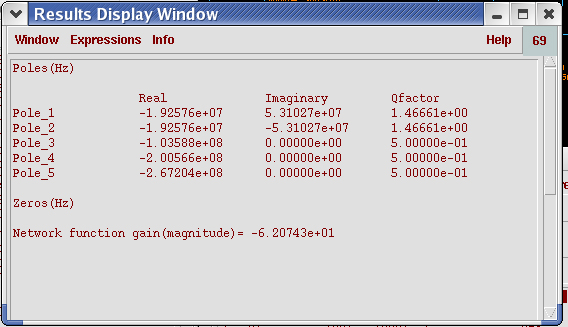
      图3 PM=45度时的极点分布

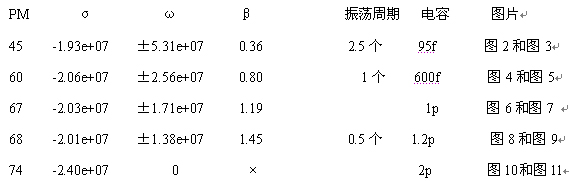
    首先来分析PM=45的情况，阶跃响应和闭环极点如图2和图3所示，系统出现了左平面上的共轭复根, 时域上出现了减幅振荡。肉眼能分辨的震荡包括三个上凸，两个下凹，最后一个上凸不很明显，合共2.5个振荡周期T,这可以说明什么呢？ 其实一旦出现减幅振荡，理论上再过10年，振荡也不会变为0 ，但无论是考虑到噪声也好，波形软件能够到达的精度也好，减幅振荡一旦衰减到一定的程度，例如1% ， 就能够认为振荡消失了。可以尝试计算下经过一个振荡周期波形能衰减到多少。 这里经过的时间为t=2.5T，由公式1 和公式2 及 β=0.36 可得t=2.5T=2.5×0.36 ×2π×τ =5.7×τ , 就是说指数项经过5.7τ的衰减变为原来的exp(σ×5.7×τ)=0.3% ,这说明指数衰减到约0.3%后，减幅震荡就消失了。



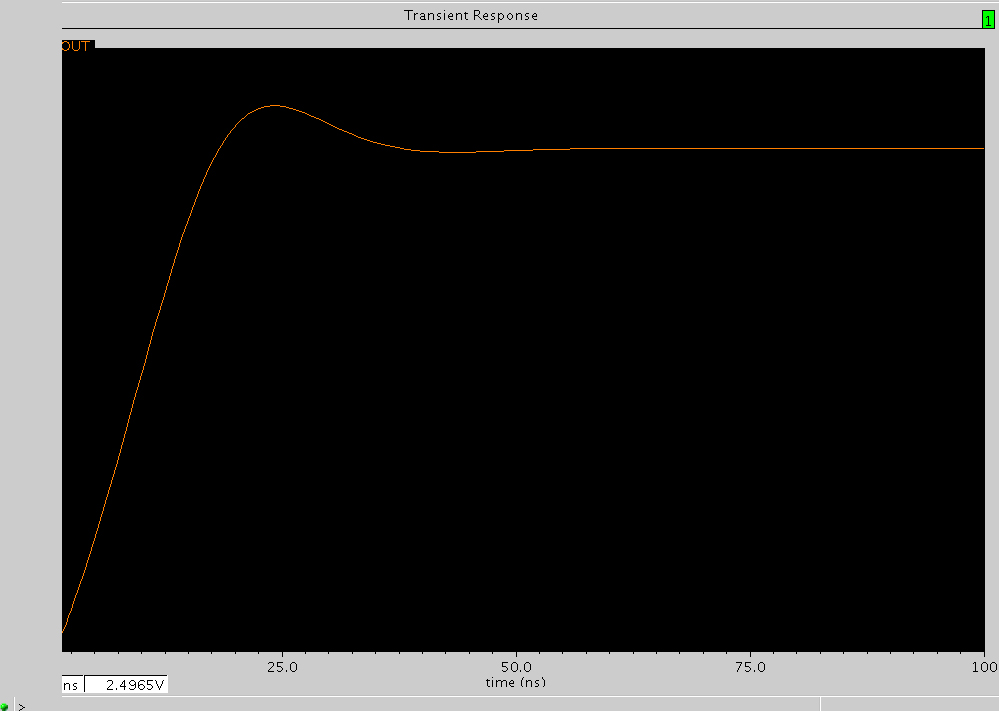
      图4 PM=60度时的阶跃响应



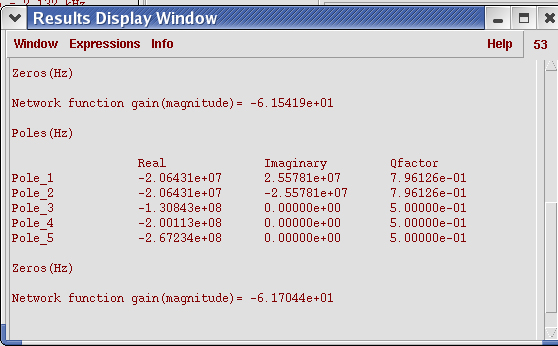
       图5 PM=60度时的极点分布

    接着来看PM=60的情况(图4和图5)，β = 0.8 , 刚好比PM=45的β=0.36两倍稍微大一点， 这说明同样要衰减到震荡消失,例如同样经历5.7τ后衰减到0.3%，PM=45的振荡周期理论上应该为PM=60的2.2倍。我们看图4来验证这一点，PM=60时有一个过冲的上凸和一个不明显的下凹，合共一个振荡周期，而PM=45的情况下震荡了2.5个周期。





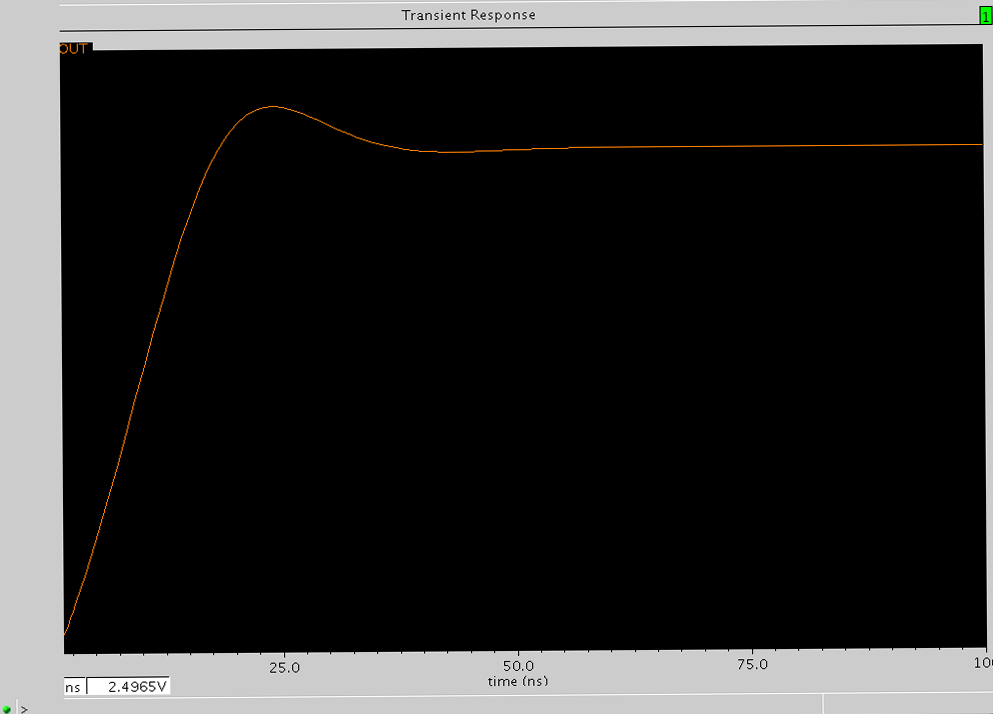
    图6 PM=67度时的阶跃响应





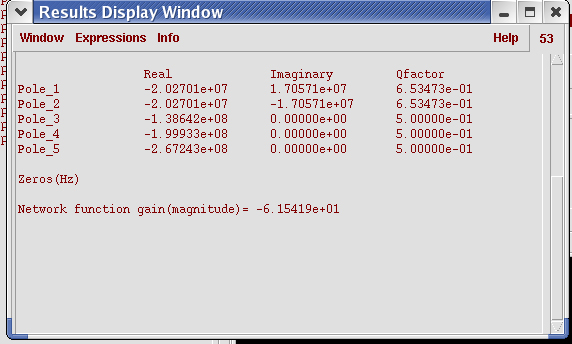
图7 PM=67度时的极点分布





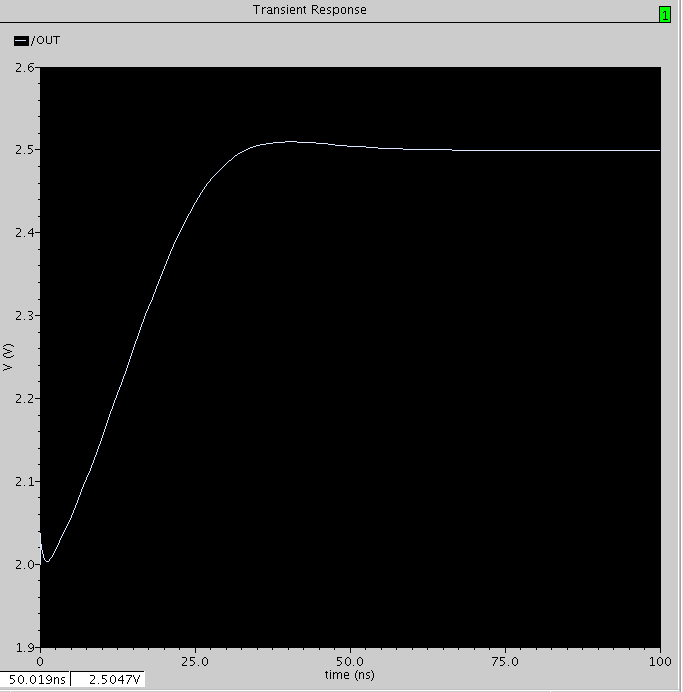
               图8 PM=68度时的阶跃响应





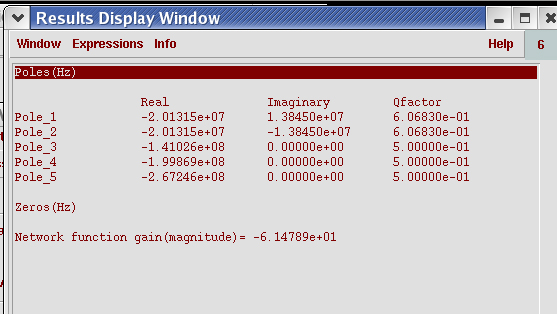
               图9 PM=68度时的极点分布

    如图8所示，在开始的半个周期内（上凸的那一段），就已经被衰减到零了，还来不及开始下半周期(下凹)的振荡。下面可以按PM=45的情况为标准，振荡刚好为0.5T的β理论上应该大概是PM=45时候的5倍，那就是0.36×5=0.18 ,以PM=68的情况和图D1和D2为例子，实际的β=1.45 , 说明由于其它极点的影响，振荡周期太少的话，振荡的波形变得较难辩认，这种相互间比例计算误差变大。





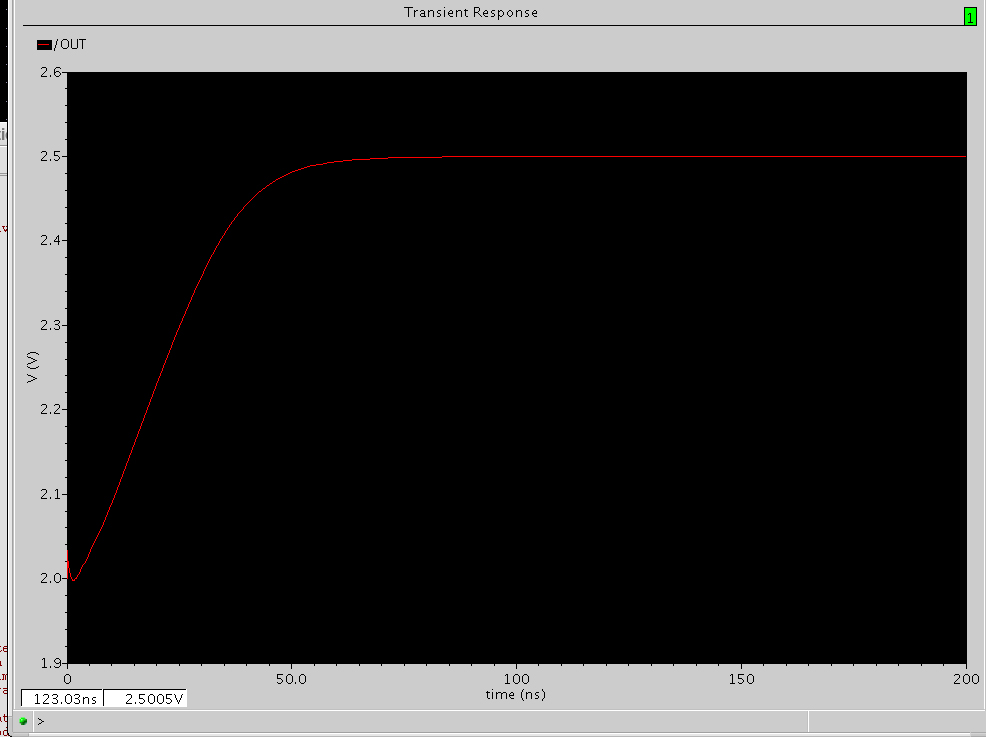
            图10 完全没有振荡时的阶跃响应




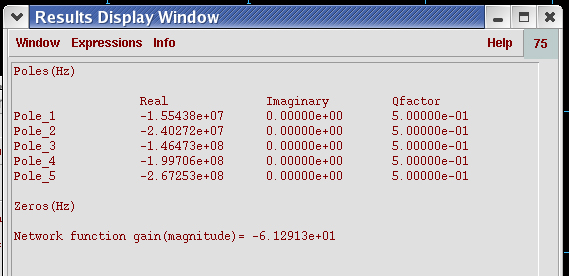
                 图11 完全没有振荡时的极点分布

    最后，当PM调为74时，由图10和图11可以看出，闭环AC也没有了共轭复极点，对应的阶跃响应也没有了过冲和减幅振荡。

    所以产生了减幅振荡和不稳定并不是等同的，在我的理解里，稳定等同于没有振荡或者衰减得很快的减幅振荡。相位裕度和稳定性并没有完全的对应关系。如表1所示，系统的稳定性是和闭环极点位置直接关连的。用系统开环的波特图曲线和相位裕度去推导闭环的零极点分布，去分析稳定性，能有百分百确定的结果吗？这是相位裕度的一个局限的方面.
       从表2上可以看出，对于衰减振荡，β的值越大 ， 系统就越倾向于稳定，因为衰减因子越大，振荡衰减得越快，而振荡频率ω越高，在衰减的过程中振荡的次数就越多,就越不稳定。对于exp(σt) × sin(ωt)这个指数正弦项，假设经过5个τ的衰减，振荡消失。将σ变为原来的十倍，由于τ变为原来的十分之一，所以衰减的时间也变为十分之一，衰减过程中振荡的周期次数也变为原来的十分之一。假设将ω增大十倍，同样的5个τ时间内，振荡的周期次数增加到原来的十倍。所以σ和ω的值对稳定性的影响是等价的, 系统走向稳定，或者不稳定，取决于σ与ω的比值β

       在产生了减幅振荡时, β和稳定性的关系还可以从另为一个方面证明。其实这个β就是s平面极点到坐标原点斜率slope绝对值的倒数。打开拉扎维书上P458 , 图15.37二型锁相环的根轨迹。在K增大时，极点沿着轨迹圆向左移动slope的绝对值不断减少，同时稳定性不断增加，这个可以从对应的P457页的波特图可以看出。给大家留个思考问题，图15.37的上半圆的曲线上升部分，σ与ω都在增加，稳定性为什么会增强？上半圆的曲线下降部分，σ与ω都在减少，稳定性为什么会继续增强？开始感到有点意思了吧。

       就像相位裕度45度和60度一样，我认为，闭环系统存在左平面上的共轭复极点时，只要β=0.36就接近一般概念上的相位裕度45度的稳定性,β=0.8就接近一般概念上的相位裕度60度的稳定性, 要达到更高的稳定性，需要更高的β值。若是闭环系统不存在共轭复极点，则阶跃响应应没有过冲和减幅振荡。

      在存在减幅震荡时，这种方法对稳定性的描述是较线性的，例如一般概念上的相位裕度60度比45度要稳定，但是到底稳定多少？曲线会平滑多少？15度？相位裕度分析只能给出大概的稳定性变化方向，不能线性的量化这个稳定性。β值就可以较线性的量化这个稳定性，这里指出 ，一般概念上的PM=60（β=0.8）的稳定性约是PM=45（β=0.36）的两倍。回想起拉杂维书上提到过一般PM=45就可稳定，但考虑到工艺角等变化推荐PM=60度，那就是说，拉杂维推荐把稳定性增强一倍来适应这些工艺角等的变化。若在设计中觉得PM=60度太奢侈，可以尝试着选择β=0.6等值。

    对比表1 ，可以思考下PM=67和PM=68的情况，相位裕度只差1度，但β值从1.19变化到1.45 , 和电容从1p变化到1.2p的比例基本一致，那个能更好的反映稳定性？

    还有， PM=60和PM=67的阶跃波形图4和图6相差很小，相位裕度和β值却相差很多。当你设计一个运放，把运放的相位裕度改善很多，但在时域阶跃仿真的时候却发现波形变化很小，并感到迷惑的时候，查看β值可以省下你的眼力，再不用盯着屏幕上的波形去辨认出那些小变化。当你要在衰减振荡3，4次的情况下多次调节电路的稳定性，并做出阶跃检验的时候，会体会到β的好处的，那就是不用每一次仿真之后都要比较那些波形。



下面是总结三种仿真方法的优缺点


相位裕度分析      
    优点 ： 能反映开环系统零极点，带宽，增益变化,输出阻抗等对稳定性的直接影响,对调节电路最有帮助         
    缺点 :和稳定性没有完全的对应关系 ，大多时候能行

闭环极点法        
    优点 ： 揭示闭环系统稳定性的本质，和稳定性有完全的对应关系，能较线性地量化存在减幅震荡时的稳定性
        缺点 :      不能反映开环系统零极点，带宽，增益变化等对稳定性的直接影响
  
电路时域阶跃仿真  

    优点 ： 最接近和最能反映真实电路的性能，包括大信号特性，和稳定性有最完全的对应关系            
       缺点 :不能反映开环系统零极点，带宽，增益变化等对稳定性的直接影响,  比较表面化，不能很好的理解仿真结果


     最后，给出闭环极点法的限制：在系统出现减幅振荡时，共轭极点要在实部绝对值最小的三个极点中的两个，即离jw轴距离最近的三个极点中的两个。

当系统出现减幅振荡时，振荡部分的波形无论在延迟时间，还是幅度上都会占据阶跃响应的主特性，在阶跃响应上清晰的表现出来，从而成为我们判断稳定性的依据，为什么不可以直接描述这个振荡呢？

dscd1900

谢谢你啊楼主，简直耳目一新，如沐春风，你的方法对于理解二阶系统时频域的对应关系非常有帮助，TKS

hebut_wolf

这个得顶！

smile962

不错，谢谢！！

ilikeeatingcake

32# guang3000
相位裕度与瞬态响应本来就是tradeoff。LDO需要调的不仅仅是PM，PM只是必要条件。

guang3000

   

个人感觉，楼主非常有创新精神，分析也很有道理。
做学术发表应该很好，但还有待楼主进一步分析
不足点：
先不说而楼主的分析方法对不对，或者对CORNER的估计方便与否。大家用AC看相位裕度来估计稳定性是因为它有 ...
tayo134 发表于 2010-4-7 15:43

                               
登录/注册后可看大图

对的，这个方法是对调节电路没什么帮助，但是在其它方面可能会有用处。举个例子，在做LDO方面有相位裕度很低，例如30度，时域曲线也很平滑，可以去流片。例如某天两位做LDO的人相遇了，他们如何去描述他们各自做的LDO的稳定性呢？曲线很平滑，平滑到什么程度？曲线过冲很小，又会小到什么程度？没什么振荡，又会到什么程度。例如他们做的是不同结构的LDO ， 相同的相位裕度下，又会有近似的稳定性吗？时域的波形用人眼是比较难分辨的。同一个运放，今天调到60度，一个月后调到55度，设计者能轻易判断波形上的区别吗！或者这个方法对描述波形有一定的帮助。

jasenlee

支持楼主！！

jiang1117

youdianyun   haah

ss758

请问图3的零极点列表是怎么生成的，是有这样的命令还是自己写表达式？
谢谢

alvays

留个记号慢慢欣赏